NDA Question Paper and Answer Key of NDA 2 2017 Exam

Check out NDA 2 2017 question paper and answer key of UPSC here. Read to know the questions asked in NDA exam held on 10 September 2017 along with correct answer key.

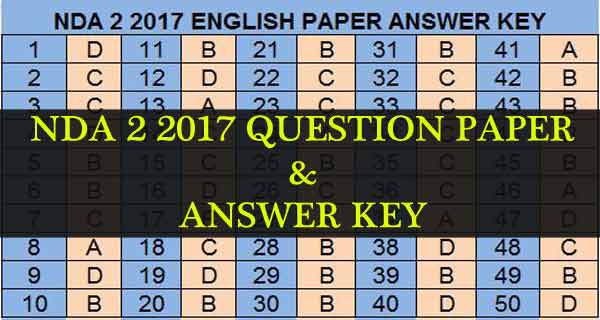
Question Paper of NDA 2 2017 Exam

NDA NA 2 2017 exam was held on 10th Septemebr 2017 by UPSC in India to shortlist potential candidates for commissioned officer posts in Indian Army, Navy and Air Force. Lakhs of students appeared in India on last Sunday.

Breakdown of GAT questions of NDA 2 2017 Question Paper

General Ability Test or GAT paper od NDA 2 2017 question paper had total 200 questions. Out of 200 questions, 50 questions were related to English. Rest 150 questions of NDA exam were related to General Awareness. Total 4 sets were provided to students appeared in the exam on Sunday.

NDA 2 2017 Question Paper Sets

• NDA 2 2017 Set A Question Paper
• NDA 2 2017 Set B Question Paper
• NDA 2 2017 Set C Question Paper
• NDA 2 2017 Set D Question Paper

NDA Question Paper Answer Key

Answer key of NDA 2 2017 question paper is very important to check how many correct answers were written by any candidate. So here we have brought out NDA 2 2017 answer key for all aspirants who have appeared in the exam held by UPSC.

NDA 2 2017 Answer Key of Set A Question Paper

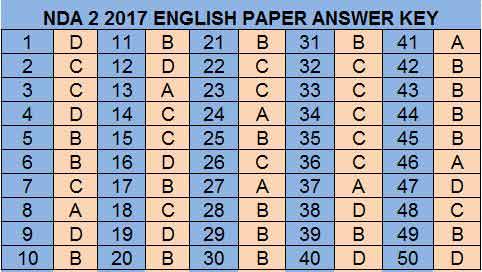
Answer Key of NDA 2 2017 English question paper

 

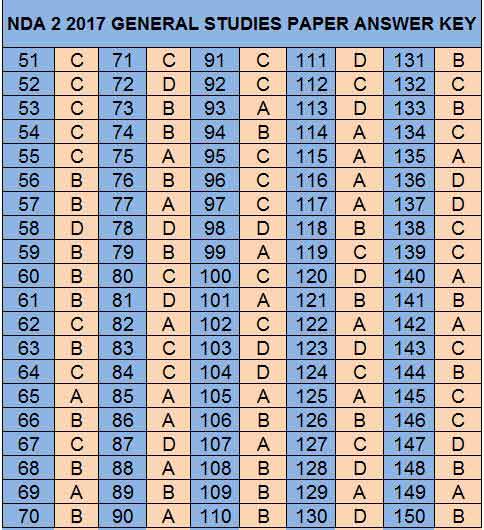
NDA 2 2017 Answers of General Ability Test

 

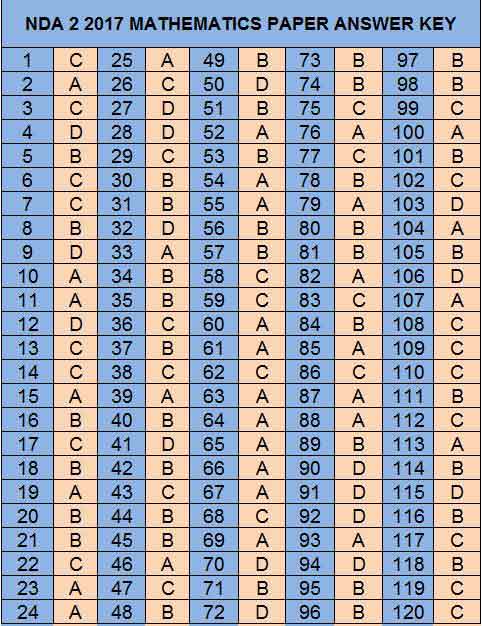
NDA NA exam answer key of Mathematics question paper

 

We are trying to upload answer keys of other NDA 2 2017 exam answer keys.

 NDA 2 2017 question paper blueprint 

1. ALGEBRA

Concept of a set, operations on sets, Venn diagrams. De Morgan laws. Cartesian
product, relation, equivalence relation. Representation of real numbers on a line. Complex numbers - basic properties, modulus, argument, cube roots of unity. Binary system of numbers. Conversion of a number in decimal system to binary system and vice-versa. Arithmetic, Geometric and Harmonic progressions. Quadratic equations with real coefficients. Solution of linear inequations of two variables by graphs. Permutation and Combination. Binomial theorem and its applications. Logarithms and their applications.

2. MATRICES AND DETERMINANTS

Types of matrices, operations on matrices. Determinant of a matrix, basic properties of determinants. Adjoint and inverse of a square matrix, Applications - Solution of a system of linear equations in two or three unknowns by Cramer's rule and by Matrix Method.

3. TRIGONOMETRY

Angles and their measures in degrees and in radians. Trigonometrical ratios. Trigonometric identities Sum and difference formulae. Multiple and Sub-multiple angles. Inverse trigonometric functions. Applications - Height and distance, properties of triangles.

4. ANALYTICAL GEOMETRY OF TWO AND THREE DIMENTIONS

Rectangular Cartesian Coordinate system. Distance formula. Equation of a line in various forms. Angle between two lines. Distance of a point from a line. Equation of a circle in standard and in general form. Standard forms of parabola, ellipse and hyperbola. Eccentricity and axis of a conic. Point in a three dimensional space, distance between two points. Direction Cosines and direction ratios. Equation of a plane and a line in various forms. Angle between two lines and angle between two planes. Equation of a sphere.

5. DIFFERENTIAL CALCULUS

Concept of a real valued function - domain, range and graph of a function. Composite functions, one to one, onto and inverse functions. Notion of limit, Standard limits - examples. Continuity of functions - examples, algebraic operations on continuous functions. Derivative of function at a point, geometrical and physical interpretation of a derivative - applications. Derivatives of sum, product and quotient of functions, derivative of a function with respect to another function, derivative of a composite function. Second order derivatives. Increasing and decreasing functions. Application of derivatives in problems of maxima and minima.

6. INTEGRAL CALCULUS AND DIFFERENTIAL EQUATIONS

Integration as inverse of differentiation, integration by substitution and by parts, standard integrals involving algebraic expressions, trigonometric, exponential and hyperbolic functions. Evaluation of definite integrals - determination of areas of plane regions bounded by curves - applications.
Definition of order and degree of a differential equation, formation of a differential equation by examples. General and particular solution of a differential equations, solution of first order and first degree differential equations of various types - examples. Application in problems of growth and decay.

7. VECTOR ALGEBRA

Vectors in two and three dimensions, magnitude and direction of a vector. Unit and null vectors, addition of vectors, scalar multiplication of a vector, scalar product or dot product of two vectors. Vector product or
cross product of two vectors. Applications- work done by a force and moment of a force and in geometrical problems.

8. STATISTICS AND PROBABILITY

STATISTICS: 

Classification of data, Frequency distribution, cumulative frequency distribution - examples. Graphical representation - Histogram, Pie Chart, frequency polygon - examples. Measures of Central tendency - Mean, median and mode. Variance and standard deviation - determination and comparison. Correlation and regression.

PROBABILITY: 

Random experiment, outcomes and associated sample space, events, mutually exclusive and exhaustive events, impossible and certain events. Union and Intersection of events. Complementary, elementary and composite events. Definition of probability - classical and statistical - examples. Elementary theorems on probability - simple problems. Conditional probability, Bayes’ theorem - simple problems. Random variable as function on a sample space. Binomial distribution, examples of random experiments giving rise to Binominal distribution.